News
June, 2025
New paper: Koylu, C., Kasakoff, A.B., & Torkashvand, M. (2025). US migration from 1850 to 1920: A comparison of family trees with linked census data
PDF
https://doi.org/10.1080/01615440.2025.2516022
April, 2025
We are excited to announce the launch of theCancer Analytics & Maps for Small Areas (CAMSA) in Iowa Cancer Registry.
Funded by the National Cancer Institute (NCI), CAMSA is an interactive mapping tool to visualize cancer data at the ZIP code and county levels based on user-centered design.
New collaborative paper:
Rethinking GIScience Education in an Age of Disruptions
https://doi.org/10.1111/tgis.70048
December, 2024
New paper: Koylu, C., & Kasakoff, A. B. (2025). Ethical Challenges in Analyzing and Mapping Historical Demographic Changes and Migration Using Population-Scale Family Trees
PDF
https://doi.org/10.14714/CP105.1945
November, 2024
Caglar presented a paper at SSHA 2024 in Toronto, CA:
Proximity of Parents to Their Adult Children in the United States in 1880: Evidence from Family Trees
October, 2024
Loretta presented Roots & Migrants: A user-centered story map application for understanding and teaching
historical population dynamics and migration in the U.S. at NACIS 2024 in Tacoma, WA.
New collaborative paper:
A research agenda for GIScience in a time of disruptions
September, 2024
Dr. Kwon started as an Assistant Professor of Geospatial Science at Lehman College!
August, 2024
As part of the NSF-funded BluGAP project, Maryam developed the
“Rivers and Risks” interactive story map
to bridge the gap between spatial analysts and watershed communities and foster collaboration in river protection.
July, 2024
Ariana Luan, Devesh Aggarwal, and Sumin Bae, our high school researchers, joined our lab this summer to participate in the Secondary Student Training Program (SSTP) at the University of Iowa.
June, 2024
On June 26, 2024, The Geo-Social Lab hosted the first NSF-sponsored workshop connecting high school teachers and students for the development of "Roots & Migrants", an online educational tool for enhancing public scientific literacy on U.S. history, migration, and kinship networks.
CaGIS+UCGIS Symposium at The Ohio State University, Columbus, OH
Caglar participated on a panel about the curriculum needs that can respond to and shape the direction of GIScience in an age of scientific disruption.
Maryam won the best student paper award with her paper on
'A Hierarchical Approach for Geocoding Birthplaces in Temporally Continuous Crowd-Sourced Family Tree Data'.
Jinyi presented our research on
'Social Vulnerability and Exposure to Private Well Nitrate Contamination in Iowa: An Interpretable Machine Learning Approach'.
April, 2024
Caglar presented our paper on Analysis of U.S. Internal Migration Using Population-Scale Family Tree Data, 1850–1920 at PAA 2024, April 18, Columbus, OH.
March, 2024
New article by Caglar and Alice: Population-scale kinship networks
PDF
https://doi.org/10.1002/9781118786352.wbieg2193
December, 2023
New paper: Andris, C., Koylu, C. & Porter, M.A. (2023). Human-network regions as effective geographic units for disease mitigation
PDF
https://doi.org/10.1140/epjds/s13688-023-00426-1
November, 2023
New paper: Kwon, H., Koylu, C. Revealing associations between spatial time series trends of COVID-19 incidence and human mobility: an analysis of bidirectionality and spatiotemporal heterogeneity
PDF
https://doi.org/10.1186/s12942-023-00357-0
Maryam and Caglar presented papers at SSHA 2023:
Evaluation of the child-ladder method for studying migration using family trees: A comparison with linked U.S. census data, 1850 to 1920
Linking family trees with the 1880 U.S. Census Records
October, 2023
Jinyi presented her research on the Curriculum Design of Artificial Intelligence and Sustainability in Secondary School at the I-GUIDE Forum 2023, October 4, 2023, New York, NY.
Read the conference proceeding
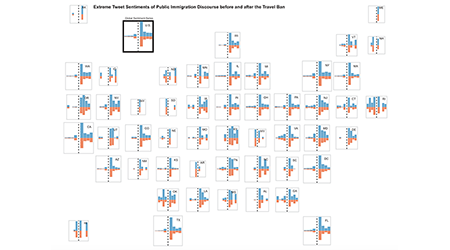
Hoeyun published the first paper of her dissertation,
"Natural language processing meets spatial time series analysis and geovisualization:
Identifying and visualizing spatio-topical sentiment trends on Twitter",
in Cartography and Geographic Information Science.Preprint available
Caglar presented FlowMapper.org: Flow Mapping Made Easy! at NACIS 2023 Practical Cartography Day in Pittsburgh, PA.
Watch the presentation on YouTube
September, 2023
Caglar gave a seminar “Giant Family Trees in Human Geography: Preliminary Results from US 1789 to 1930”, at University College London, UK.
Caglar presented the paper co-authored with Maryam "The effect of disruptive events on spatial and social interactions:
An assessment of structural changes in pre-and post-COVID-19 pandemic networks” at the
GIScience 2023 Workshop on Disruptive Movement Analysis (DMA’23), Leeds, UK.
August, 2023
Kelvin Liu and Kevin (Rongxuan) Zhu, our high school interns, joined our lab this summer to participate in the Secondary Student Training Program (SSTP) at the University of Iowa.
Click for Kelvin's research poster!
Click for Kevin's research poster!
May, 2023
Hoeyun succesfully defended her Ph.D. on May 8, 2023, and is now a Ph.D! Congrats Dr. Kwon!
Dr. Kwon will continue her journey as a postdoc in University of Colorado Boulder!
Learn more about Hoeyun!

January, 2023
Caglar was elected as the Vice President of Cartography and Geographic Information Society (CaGIS)!
Read More
November, 2022
Hoeyun Kwon presented our research on the unequal impact of COVID-19 by analyzing the mobility behaviors of socially vulnerable populations at the AutoCarto 2022 conference held at Redlands, CA.
Watch the presentation on YouTube
Maryam presented our research on mapping migration regions and their evolution from population-scale family trees at The 6th ACM SIGSPATIAL Workshop on Geospatial Humanities (GeoHumanities’22), November 1, 2022, Seattle, WA.
Read the conference proceeding
October, 2022
Caglar presented FlowMapper at NACIS 2022 in Minneapolis.
Watch the presentation on YouTube
Caglar participated on a panel about multigenerational households on ABC/Channel 9 on "Ethical Perspectives On the News" moderated by Leon Tabak.
Watch the panel on YouTube!
September, 2022
Super excited to announce NSF funding ($477,734) of our project on population-scale kinship networks and migration!
Public abstract
August, 2022
Welcome to Fall 2022 and our new Ph.D. Student, Maryam Torkashvand!

July, 2022
Adelina Chau and Jonathan Fan, our high school interns, joined our lab this summer to participate in the Secondary Student Training Program (SSTP) at the University of Iowa.
Click for Adelina's research poster!
Click for Jonathan's research poster!
June, 2022
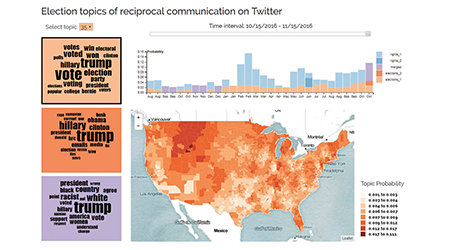
Our paper
"Recreating Human Mobility Patterns Through the Lens of Social Media:
Using Twitter to Model the Social Ecology of Crime"
has been published in Crime & Delinquency.Preprint available
|
May, 2022
Very excited to collaborate with Jacob Oleson (Biostatistics) on National Cancer Institute (NCI) funded project ($1,188,804), "Development of Small Area Interactive Risk Maps for Cancer Control Efforts".
Public abstract
April, 2022
Hoeyun Kwon won the prestigious Doctoral Scholarship Award of 2022 by the Cartography and Geographic Information Society (CaGIS)! Congrats Hoeyun!
March, 2022
Hoeyun Kwon won the second place in GIS Specialty Group Student Honors Paper Competition at AAG 2022! Congrats Hoeyun!
February, 2022
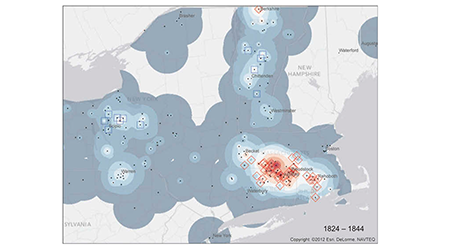
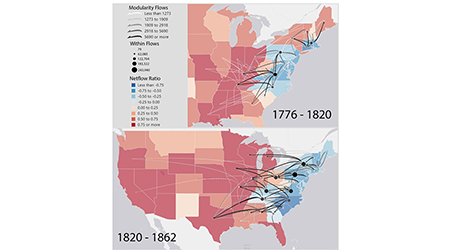
Our paper "Measuring and mapping long-term changes in migration flows using population-scale family tree data" have been featured on the cover of Cartography and Geographic Information Science!
|

|
January, 2022
Our papers "Measuring and mapping long-term changes in migration flows using population-scale family tree data" and
"FlowMapper.org: A web-based framework for designing origin-destination flow maps"
have been published in Cartography and Geographic Information Science and Journal of Maps!
December, 2021
Congrats for Hoeyun Kwon for successfully defending her dissertation proposal and becoming a Ph.D. candidate!
November, 2021
Our paper "Measuring and mapping long-term changes in migration flows using population-scale family tree data" has been accepted for publication in Cartography and Geographic Information Science!Preprint available
October, 2021
Our paper "FlowMapper.org: A web-based framework for designing origin-destination flow maps" has been accepted for publication in Journal of Maps! Check Flowmapper!
Check out the preprint!
September, 2021
Hoeyun Kwon presented our research on the relationship between human mobility and COVID-19 prevalence at GIScience 2021 workshop on Advancing Movement Data Science (AMD’21).
Click for Hoeyun's blog post!
Geng Tian updates us on how he is doing in China, working on a very cool project - unmanned vehicles delivering food!
Click for Geng's blog post!
August, 2021
Kaitlyn Hom and Mark Rifkin, both senior high school students, joined our lab this summer to participate in the Secondary Student Training Program (SSTP) at the University of Iowa.
Click for Kaitlyn's blog post!
Click for Mark's blog post!
Angelina Evans worked as an intern in the US Department of Energy's prestigious Science Undergraduate Laboratory Internship (SULI)
program in the Geospatial Science and Human Security Division at Oak Ridge National Laboratory (ORNL).
Click for Angelina's blog post!